Review the Graphs of Linear Equations Using Standard Form and Intercepts Worksheet
Keep reading to review the standard form of a linear equation. We'll learn why we utilize the standard form of linear equation as well as how to write equations and graph with the standard form. Lastly, we will review other forms of linear equations.
Using our hands, we can alter a piece of clay into a piece of work of art. As well, using our mathematical tools, we tin can change an equation into a different form. The unlike forms provide us with useful data.
At present, let'due south dive into standard form!
What is the standard form of a linear equation?
The standard form of a linear equation, too known as the "full general grade", is:
ax+past=c
The letters a, b, and c are all coefficients. When using standard form, a, b, and c are all replaced with real numbers. The alphabetic character x represents the independent variable and the letter y represents the dependent variable.
A few notes on Standard Grade:
- The a term must be a positive integer
- a, b, and c cannot be decimals or fractions
Render to the Table of Contents
Why utilise standard grade?
The standard grade of a line can exist particularly helpful when solving a organisation of equations. For instance, when using the elimination method to solve a organisation of equations, we can easily align the variables using standard form.
System of equations with standard form
Let'due south see a quick example. If we were given the organisation of equations:
y=-4x+nine
y-ix=\frac{1}{2}ten-4
…we tin rewrite the equations in standard form.
y+4x=9
2y-x=10
Then, nosotros can solve using the elimination method by multiplying the 2nd equation by 4.
y+4x=ix
8y-4x=40
By calculation these equations together we obtain: 9y=49. When we solve that, we know y=\frac{49}{9}.
Then, we can substitute the value of y into i of the original equations to determine the value of x.
2y-x=10
2(\frac{49}{9})-x=ten
(\frac{98}{9})-x=10
-ten=ten-(\frac{98}{nine})
10=-x+(\frac{98}{ix})
10=\frac{8}{9}
Now we have solved the arrangement of equations. The solution is (\frac{8}{ix},\frac{49}{9}) . Using standard form allowed us to use the elimination method to solve the system.
Equally we'll see beneath, standard form is also useful for easily determining the intercepts of a linear office.
Return to the Tabular array of Contents
How to write a linear equation in standard form (example)
Allow'due south write an equation of the line with a slope of 4 and a y-intercept of seven in standard class.
To brainstorm, we volition start write the equation in slope-intercept form. This is the easiest form to write when given the slope and the y-intercept.
y=mx+b
Nosotros know the slope, grand, is 4 and the y-intercept, b, is seven.
y=4x+vii
To change this into standard class, all nosotros need to do is subtract the 10 term from both sides, in this case 4x.
y-4x=vii
We take now written the standard from of a linear equation. The linear equation with a slope of 4 and a y-intercept of 7 is y-4x=7.
Are you more than of a visual learner? Checkout the video below with another case of writing linear equations in standard form:
Render to the Table of Contents
How to graph a standard class linear equation (example)
Nosotros also need to know how to graph a standard course equation. In standard form, we can easily determine the x and y-intercepts.
Allow's graph the equation 3y-5x=30.
Discover x-intercept
Starting time, we can determine the ten-intercept. Remember, this is where the line crosses the x-axis and where y=0. To do so, we volition substitute 0 for y.
3y-5x=30
iii(0)-5x=thirty
-5x=30
10=-6
Therefore, the x-intercept is at -six. This means the point (-half dozen,0) is on the graph.
Find y-intercept
Let united states of america now determine the y-intercept. Remember, this is where the line crosses the y-centrality and where x=0. To do and so, we volition substitute 0 for x.
3y-5x=30
3y-5(0)=xxx
3y=xxx
y=ten
Therefore, the y-intercept is at 10. This means the point (0,10) is on the graph.
Draw the graph
Nosotros now plot the x and y-intercepts. We are plotting the points (-6,0) and (0,10).
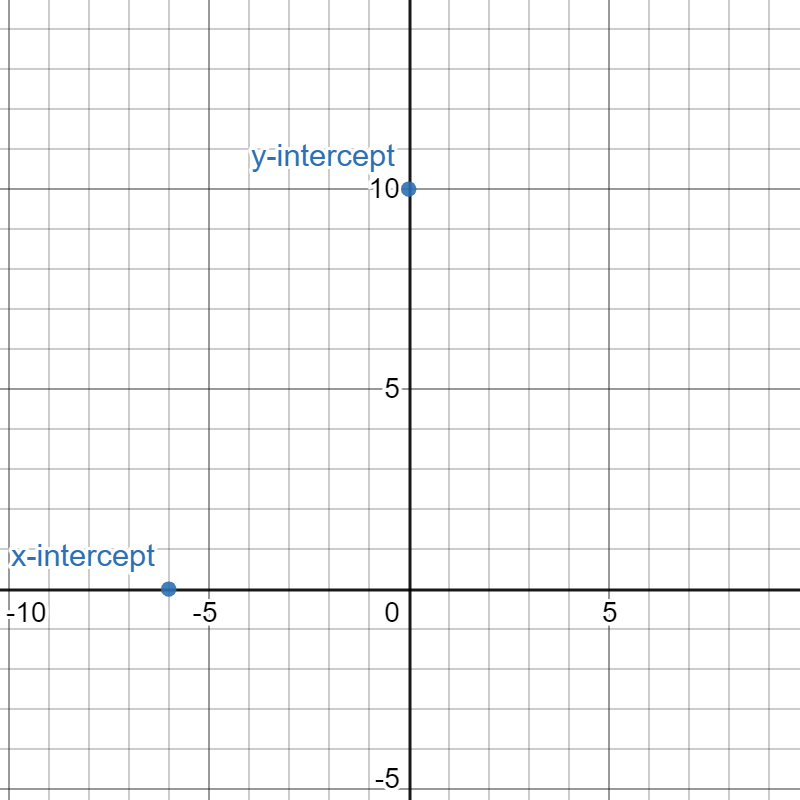
The very concluding step is just to connect the points on the graph. This creates the graph of the standard form equation 3y-5x=30.
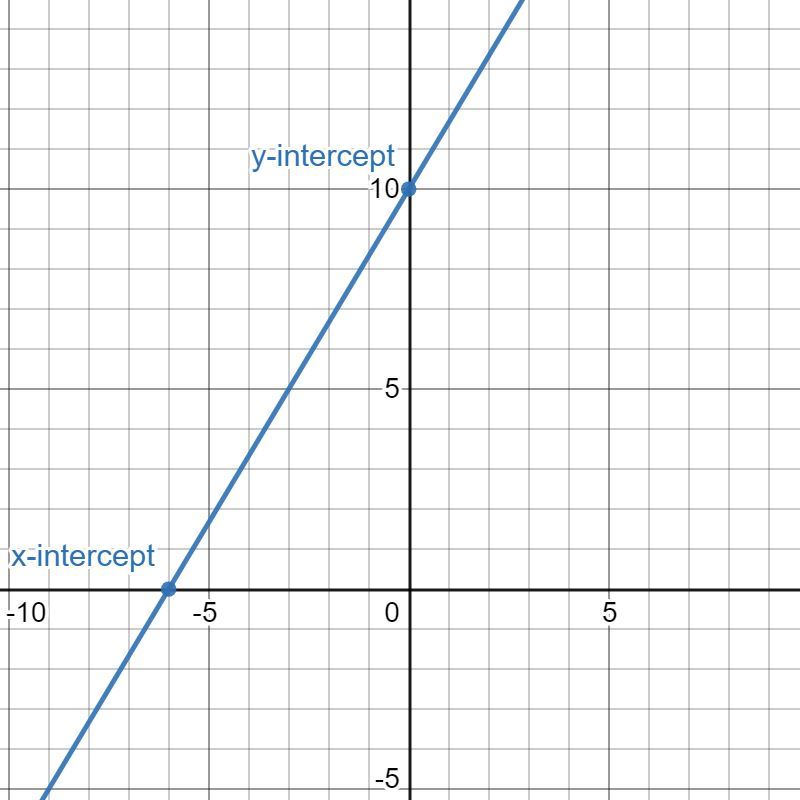
Now you lot know how to graph a standard form equation!
To view another example of graphing from standard form, check out the video beneath:
Render to the Table of Contents
Other forms of linear equations
Slope-Intercept Course
Linear equations can be written in slope-intercept form, determined past the gradient and the y-intercept of a line. For more info, visit our review guide on slope-intercept class.
Slope-Intercept Form
y=mx+b
Signal-Slope Course
A linear equation can also exist written in point-slope form. This form is determined by one point and the slope of the line. For more details, read our point-slope review guide.
Point-Slope Form
y-y_1=m(x-x_1)
Return to the Table of Contents
Summary: Standard Form
In this review post, we've learned:
- Standard course of an equation is: ax+past=c
- Standard form is useful for solving systems of equations and for determining intercepts
- How to write a linear equation in standard grade
- How to graph an equation in standard form
Click here to explore more helpful Albert Algebra 1 review guides.
Return to the Table of Contents
Source: https://www.albert.io/blog/standard-form-of-linear-equation/
0 Response to "Review the Graphs of Linear Equations Using Standard Form and Intercepts Worksheet"
Post a Comment